0. 目錄

• VDOC_05_Python_Scipy
  • 0. 目錄
  • 1. 老駱提醒
  • 2. 問題描述
  • 3. Python Scipy
  • 4. 聯絡老駱

1. 老駱提醒

• 請先確認，您已經閱讀 VDOC_00_Introduction 中的聲明。
• 本文補充說明如何利用Python Scipy進行函數最小化求解。

2. 問題描述

Minimize Objective Function $f(x,y)$:

$$f(x,y) = {(x^2 + y^2) \over 10} - \cos(x)\cos(y)$$

Subject to the Constraint Equation $g(x,y)$:

$$g(x,y) = (x^2 + y^2) \ge 1.5$$

Design Variables (Side Constraints):

$$-2\le x\le2\\ -2\le y\le4$$

Initial Conditions:

$$x=2\\ y=2$$

3. Python Scipy

以下程式碼主要參考 Scipy 的教學文檔設置。

這裡老駱選擇minimize中的 trust-constr 方法，因為這個方法不用提供額外的jacobian和hessian函數即可求解，並且在option裡附有verbose選項，可以將其設為2，方便觀察求解過程。為了符合Scipy的格式，下方程式中的x[0]為問題中的x，而x[1]則為問題中的y。

from math import cos
import numpy as np
from scipy.optimize import minimize, Bounds, NonlinearConstraint

# Objective function
def prob(x):
    return (x[0]**2 + x[1]**2)/10 - cos(x[0]) * cos(x[1])

# Constraint equation
def cons_f(x):
    return x[0]**2 + x[1]**2
nonlinear_constraint = NonlinearConstraint(cons_f, lb=1.5, ub=np.inf)

# Bound of design variables
bounds = Bounds([-2, -2], [2, 4])

# Initial condition
x0 = np.array([2, 2])

# Solve the question
resp = minimize(fun=prob, x0=x0, method='trust-constr',
                bounds=bounds, constraints=[nonlinear_constraint],
                options={'verbose':2})

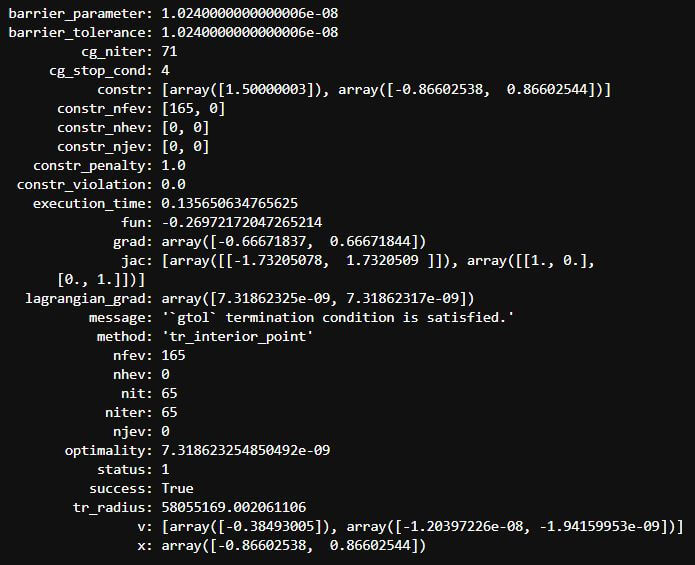
print(resp)

()內為PythonEquation被呼叫次數	x	y	f	g
Opt Using PythonEquation(48)	0.86087	0.87115	-0.26971	1.50000
Opt Using DOE(9)	2.00000	0.29777	-0.07096	4.08891
Opt Using DOE(Verified by PythonEquation)(40)	2.00000	0.29777	-0.07096	4.08891
RSA Using DOE(33)	0.86787	0.86306	-0.26985	1.49966
Opt Using localPython(48)	0.86087	0.87115	-0.26971	1.50001
Python Scipy(0)	-0.86603	0.86603	-0.26972	1.50000

可以看出Scipy與VisualDOC答案相當接近。

雖然Scipy求解出來的x為-0.86603，但觀察此問題的f及g，若將x以0.86603代入，並不會影響其值，因

• f及g的平方項 : $x^2 = (-x)^2$。
• f及g的三角函數 : $cos(x) = cos(-x)$。

最後要特別提醒的是，不同的問題各有其適合求解的算法及搭配的參數。改變求解算法及調整其所使用的參數，都可能會得到不同的答案。甚至，有時候這些答案之間，也存在一段不小的差距。此時，就是考驗使用者對問題了解的程度，從中挑出最適合的算法及參數。

4. 聯絡老駱

如果您或貴單位:

• 有導入VR&D產品的意願，但是有報價、採購及發票等問題。
• 有教育訓練或顧問需求。
• 有些建言指教。
• 想交個朋友。
  歡迎透過 camel@caeml.ai 聯絡老駱。