0. 目錄

• VDOC_06_LSDYNA
  • 0. 目錄
  • 1. 老駱提醒
  • 2. 問題描述
  • 3. 前置作業
    • 3.1 LS-DYNA K檔修改
  • 4. LS-OPT
  • 5. VisualDOC操作細節
    • 5.1 Optimization
    • 5.2 DOE
    • 5.3 Optimization Using DOE
    • 5.4 RSA Using DOE
  • 6. 結語
  • 7. 聯絡老駱

1. 老駱提醒

• 請先確認，您已經閱讀 VDOC_00_Introduction 中的聲明。
• 本文例題修改自 LS-OPT Support ，版權屬於該網站。
• 本文篇幅較長，但如果能融會貫通，相信您已經可以依樣畫葫蘆，連接你想要的程式至VisualDOC。
• 如果對不熟或沒接觸過LS-DYNA的朋友，閱讀本文可能會有些吃力。
• 如果對接觸過LS-DYNA但對LS-OPT不熟悉的朋友，可以跳過相關內容。利用LS-OPT求解的用意是，在於提供一個可與VisualDOC比較的參考答案，並不在具體上比較兩者優劣。目前老駱暫時沒有寫LS-OPT介紹的計畫，但如果您有興趣想了解，可以透過 camel@caeml.ai 聯絡老駱。如果有一定人數來信的話，老駱可以規劃一個LS-OPT的系列教學文。老駱認為LS-OPT的原理相當類似於VisualDOC裡RSA + DOE的概念。
• 在Windows環境下，使用LS-OPT version 6.0.0時，如果在Setup內，新增一變數，並手動輸入變數名超過兩個字元，程式會當掉。老駱已經有回報原廠，相信未來版次會修復。

2. 問題描述

本文例題修改自 Linear response surface with strategy Sequential with Domain Reduction (SRSM) ，是 Crashworthiness Optimization 內的一個子題。進入Download，可以下載crash_srsm.zip檔案。

因為原來的題目內牽涉到HIC的計算，雖然在VisualDOC裡面也可以實現，但本文旨在分享如何結合VisualDOC和LS-DYNA進行計算，所以老駱稍微將題目修改如下:

Minimize Objective Function:

$$Mass$$

Subject to the Constraint:

$$Intrusion < 485mm$$

Design Variables (Side Constraints):

$$1.0mm < tbumper < 5.0mm\\ 1.0mm < thood < 5.0mm\\ 1.0mm < tfront < 5.0mm\\ 1.0mm < tunder < 5.0mm$$

Initial Conditions:

$$tbumper=tupper=tfront=tunder=3mm\\ $$

• Mass計算方式為Part 2 + Part 3 + Part 4 +Part 5。

• Intrusion計算方式為nodes 167 的x位移剪去node 432 的x位移。在這裡，node 432僅是作為一參考點，因為該點是模型內較無變形的地方。

• tbumper: Part 2的厚度。

• tupper: Part 3的厚度。

• tfront: Part 4的厚度。

• tunder: Part 5的厚度。

3. 前置作業

3.1 LS-DYNA K檔修改

1. 打開main.k，修改*PARAMETER。定義Part2~Part5的厚度變數及一個設定dt的時間變數。

*PARAMETER 可以設定的變數，總共有R(實數)、I(整數)、 C(字串) 3種。

2. 剪下car5.k內的*include ../../rigid2，貼到main.k內。這個修改只是老駱個人的習慣，將barrier與car兩者分離開來。最後main.k檔應該看起來像:

*KEYWORD
*PARAMETER
rtbumper,3.0
rthood,3.0
rtfront,3.0
rtunder,3.0
rdt,5e-2
*INCLUDE
../../car5.k
*INCLUDE
../../rigid2
*END

2. 打開car5.k，刪除*DATABASE_RWFORC及*DATABASE_BINARY_RUNRSF這兩項不需要的輸出。
3. 對於這個問題僅需要t = 5e-2秒時的資訊，所以可以修改car5.k最上方幾行。

*CONTROL_TERMINATION
&dt
*DATABASE_NODOUT
&dt
*DATABASE_BINARY_D3PLOT
&dt
*DATABASE_GLSTAT_MASS_PROPERTIES
&dt
*DATABASE_SSSTAT_MASS_PROPERTIES
&dt
*DATABASE_EXTENT_SSSTAT
      9999
*SET_PART_LIST
      9999
2,3,4,5
$
$ DEFINITION OF MATERIAL     1
$

4. 指定適當的厚度變數至各*SECTION_SHELL。

*SECTION_SHELL
2,2,0.,0.,0.,0.,0
&tbumper,&tbumper,&tbumper,&tbumper,0.

*SECTION_SHELL
3,2,0.,0.,0.,0.,0
&thood,&thood,&thood,&thood,0.

*SECTION_SHELL
4,2,0.,0.,0.,0.,0
&tfront,&tfront,&tfront,&tfront,0.

*SECTION_SHELL
5,2,0.,0.,0.,0.,0
&tunder,&tunder,&tunder,&tunder,0.

至此，上述修改已經可以用於LS-OPT分析。但main.k內car5.k及rigid2被INCLUDE的路徑是../../car5.k及../../rigid2。這樣的設定方便LS-OPT分析，但不太利於使用VisualDOC，所以我們可以複製一份main.k、car5.k及rigid2至一新資料夾，然候將main.k中car5.k的INCLUDE路徑改為car5.k及將rigid2的INCLUDE路徑改為rigid2，作為後續VisualDOC分析使用。

用於VisualDOC分析的main.k檔應該會像:

*KEYWORD
*PARAMETER
rtbumper,3.0
rthood,3.0
rtfront,3.0
rtunder,3.0
rdt,5e-2
*INCLUDE
car5.k
*INCLUDE
rigid2
*END

4. LS-OPT

1. 打開srsm.lsopt，Metamodel-based維持Optimization，Strategy for Metamodel-based Optimization 維持Sequential woth Domain Reduction(SRSM)。
2. 點選Setup block將tbumper、thood、tfront、tunder的Type設為Continous、Starting設為3、Minumum設為1、Maximum設為5。
3. 將dt的Type設為Constant，維持Starting為0.05。
4. 點選Sampling crash block。Metamodel選用Radial Basis Function Network，Pointselection選用Space Filling，Number of Simulation Points維持8。
5. 點選Crash block下的Setup，在Command中輸入呼叫LS-DYNA的指令。此外，可以考慮輸入d=nodump減少輸出。
6. 點選Crash block下reponses下刪除MaxAccel、HIC 兩項。
7. 點選Optimization block，將Objectives改為Mass。點選Constraint，選擇Intrusions，設定Upper Bound為485。

()內為LS-DYNA運行次數 Unit: ton & mm	tbumper	thood	tfront	tunder	mass	disp
LS-OPT(49)	4.83	1.00	1.00	4.53	0.871	483.216

5. VisualDOC操作細節

先進行1次Baserun，看看LS-DYNA是否能夠成功求解。求解成功後的ssstat及nodout檔，將用來進行後續VisualDOC的設定。

()內為LS-DYNA運行次數 Unit: ton & mm	tbumper	thood	tfront	tunder	mass	disp
LS-OPT(49)	4.83	1.00	1.00	4.53	0.871	483.216
Baserun(1)	3.00	3.00	3.00	3.00	0.865	504.997

5.1 Optimization

5.1.1 Work Flow

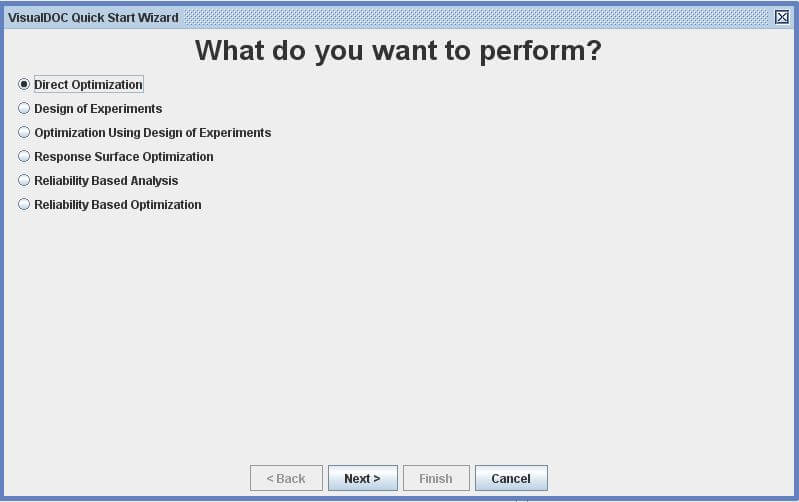
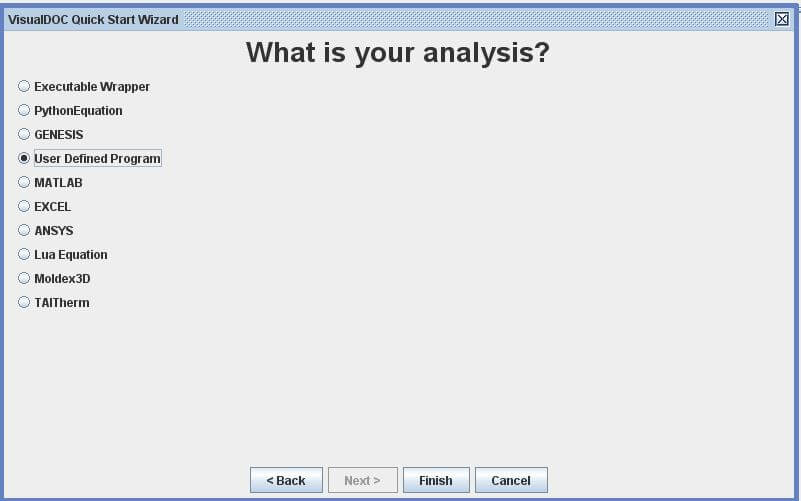
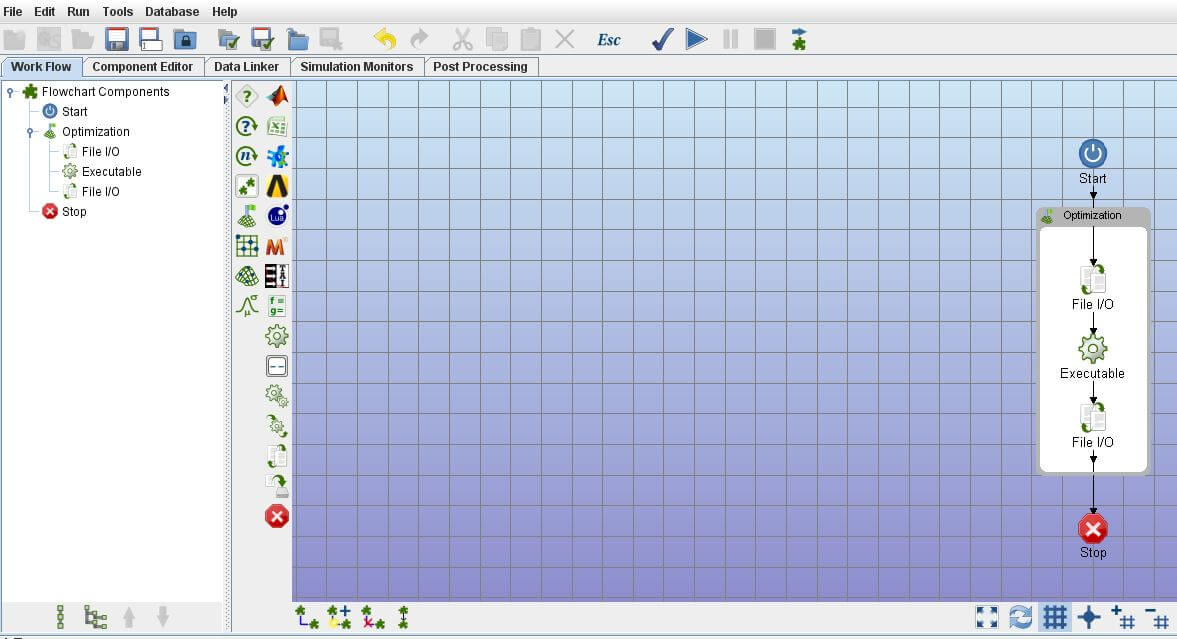
使用Quick Start->Direct Optimization->User Defined Program，快速搭建此問題的Work Flow。

5.1.2 Component Editor內層

點選C欄 Component Editor Optimization下的第一個File I/O component。

按下下方Add an input file，於File Path中選擇Main.k，VisualDOC會自動生成main.k.tmpl。

*.tmpl檔可以視為一種範本，VisualDOC將會記住這個檔案的pattern，在之後與LS-DYNA進行coupling時，可以自動替換正確的變數值給LS-DYNA求解(每次求解可以視為建立1個DOE點位)，也可以讀入LS-DYNA的結果進入VisualDOC進行後續Optimization或RSA等計算。進行*.tmpl檔設定的時候，特別要注意的是選用Format Specification時要使用Free Format或是Fixed Format。老駱一般喜歡用Fixed Format，但要特別注意數格子的時候，記得考慮變數本身的正負號也會佔一格。有時候，也會意外多含入跟隨其後數字的正負號。所以設定完之後，要記得在求解過程中觀察各個變數有沒有出現不合理的變化，通常問題都出現在最佳化求解的時候，讀入或寫出的變數有問題。

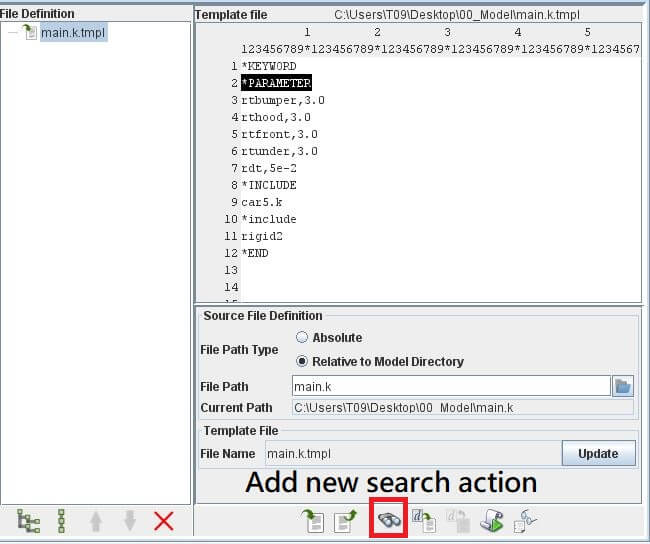
於右方Template File中點選*PARAMETER(第2行)，按下下方Add new search action。

點選rtbumper(第3行)，按下下方Add new search action。

點選rtbumper逗號後的3.0，按下下方Add new modify action。

查閱 LS-DYNAKEYWORD USER’S MANUAL VOLUME I 可以知道*PARAMETER這張卡每行有8個欄位，每個欄位可佔10格。所以可以將Format Specification設為Fixed Format，並將Fixed Length設為10，確保變數的每一個位數都能被VisualDOC找到。

依照上述邏輯，依序對rtbumper、rthood、rtfront及rtunder完成類似的設定。

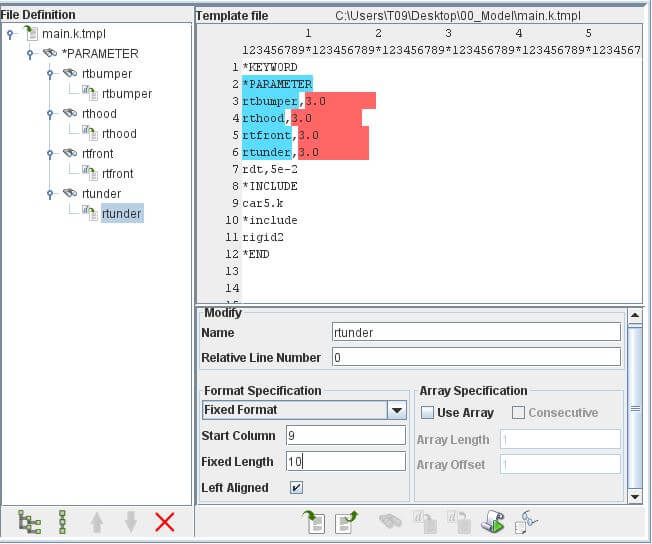
此外，也可以選擇raw array的方法，一次選取多個值，完成設定。事實上這也是Advanced Examples Manual 5.2 Coupling VisualDOC with LS-DYNA中建議的操作方式。但這麼一來，在左方的欄位將難以區分各變數，各變數名將變成t[0]、t[1]。當然，也可以在component editor外層中重新對各變數命名。一般來說，這種設定方法適用於變數很多的情況。對於變數較少的問題，老駱習慣在這邊一個一個設定，這樣一來在component editor外層也能夠不重新命名，就能從變數名識別各變數。

第一個File I/O設定完後，應該會像:

點選C欄 Component Editor Optimization下的第二個File I/O component。

按下下方Add an outout file，於File Path中選擇ssstat，VisualDOC會自動生成ssstat.tmpl。

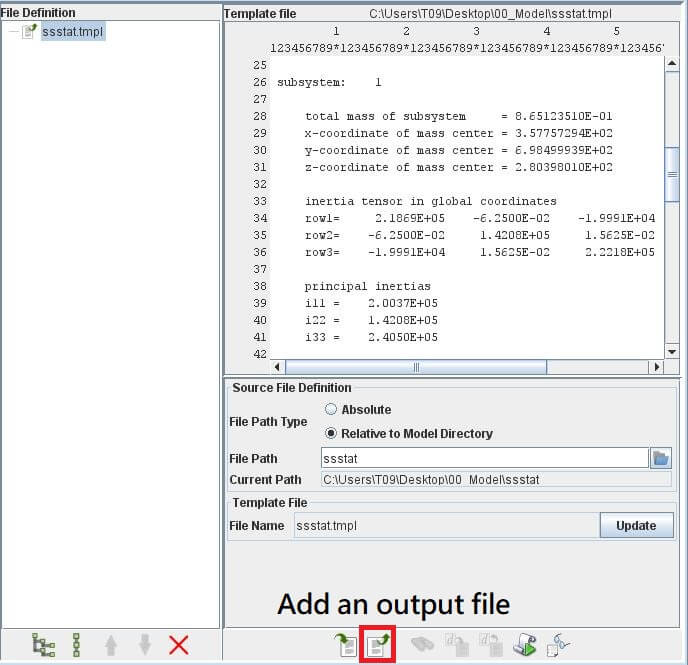
於右方Template File中點選total mass of subsystem(第28行)，按下下方Add new search action。

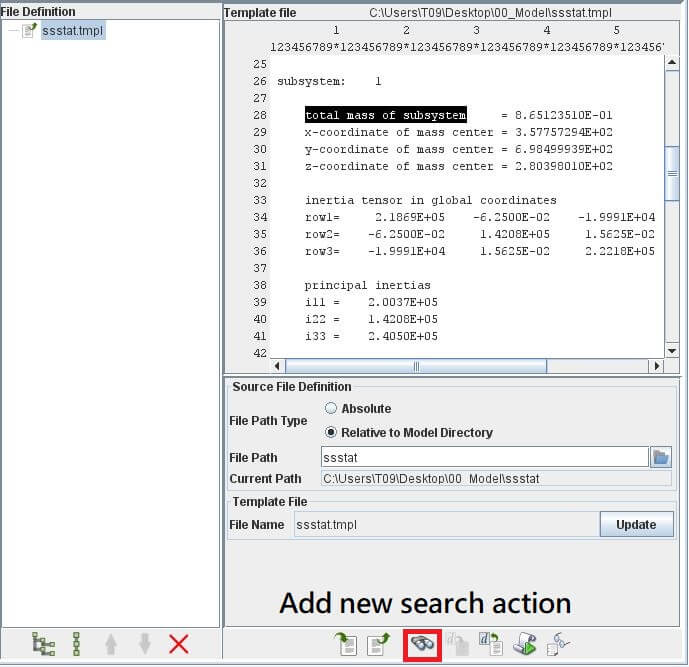
於右方Template File中點選total mass of subsystem =後的8.65123510E-01，按下下方Add new extract action。

將Format Specification設為Fixed Format，將Strarting Column設為35，Fixed Length設為16，重新命名變數名為mass。

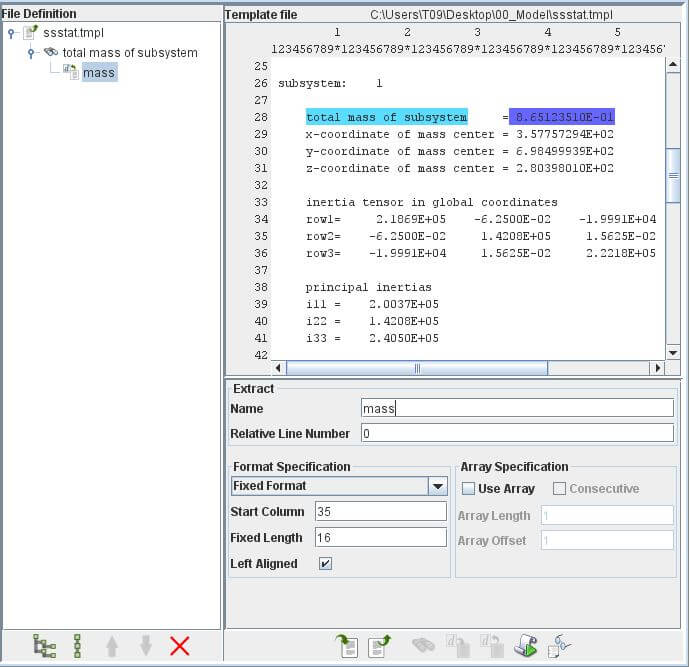
按下下方Add an outout file，於File Path中選擇nodout，VisualDOC會自動生成nodout.tmpl。

於右方Template File中點選n o d a l__p r i n t__o u t，並按下2次Find Next，此時應該能找到位於第29列的正確資訊。(注意__是代表2個空格，這是LS-DYNA nodout輸出的格式)。按下下方Add new search action。

於右方Template File中點選x-disp(第32行)，按下下方Add new extract action。重新命名變數名為disp_167_x。

有時候，*.tmpl內可能有多列都符合搜尋結果，此時就要靠Find Prev和Find Next來正確指定變數的位置。

點選Format Specification為Fixed Format，並將Start Column設為11及Fixed Length設為12。

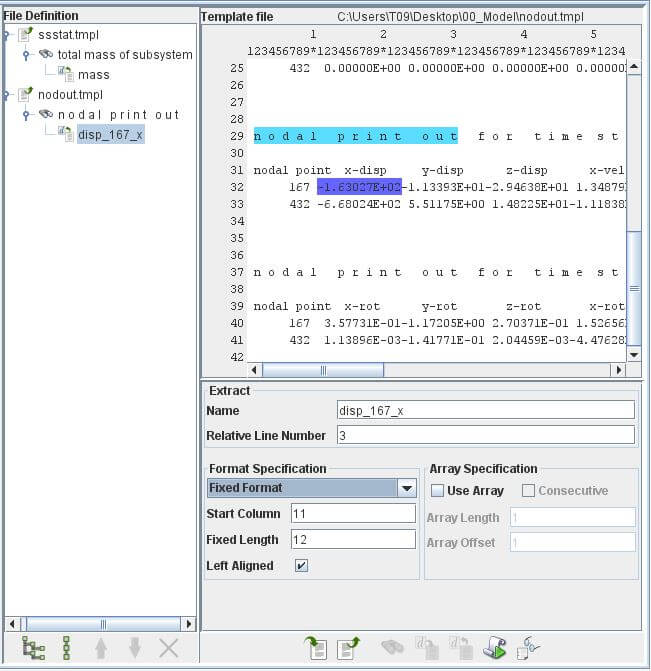
對node 432進行類似的操作，並重新命名變數名為disp_432_x

新增一個變數，命名為disp，將其Input/Output設定為Output，並將其Adv, Attribute設為Synthetic(Synthetic可以想成這個變數須要經由其它變數的運算後才能產生)。對disp_x欄按右鍵，選擇Edit dependence equation後，於上方Input輸入disp_167_x,disp_432_x，並於下方編輯區輸入disp_x = disp_167_x - disp_432_x。

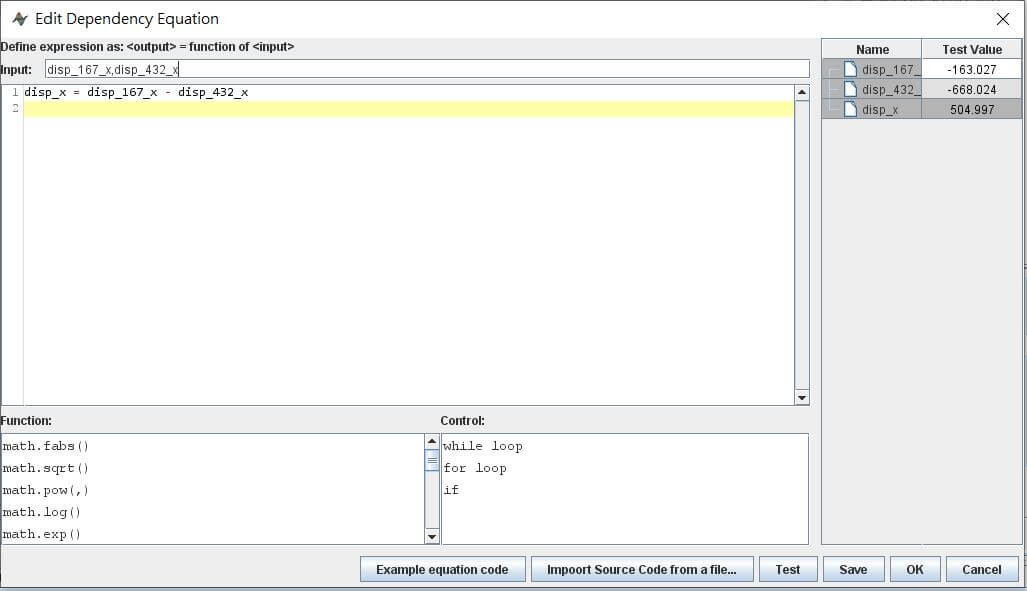
第二個File I/O設定完後，應該會像:

點選Executable component，於Local Analysis Program Definition中的File Path選擇求解器的位置，老駱自己是習慣使用環境變數，您也可以直接用路徑來選擇求解器。另外可以在Program Arguments裡輸入求解的選項，老駱這邊設定想求解的檔案名為main.k，用4個cpu求解，並且不須要產生dump file。

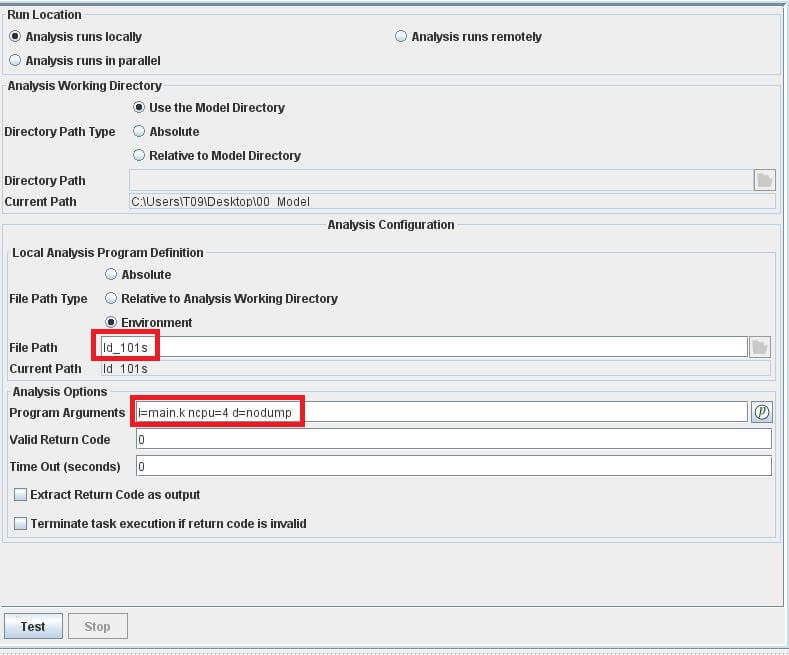
5.1.3 Data Linker

點選C欄中的Data Linker，使用Automatically add data to the selected model來自動連接。

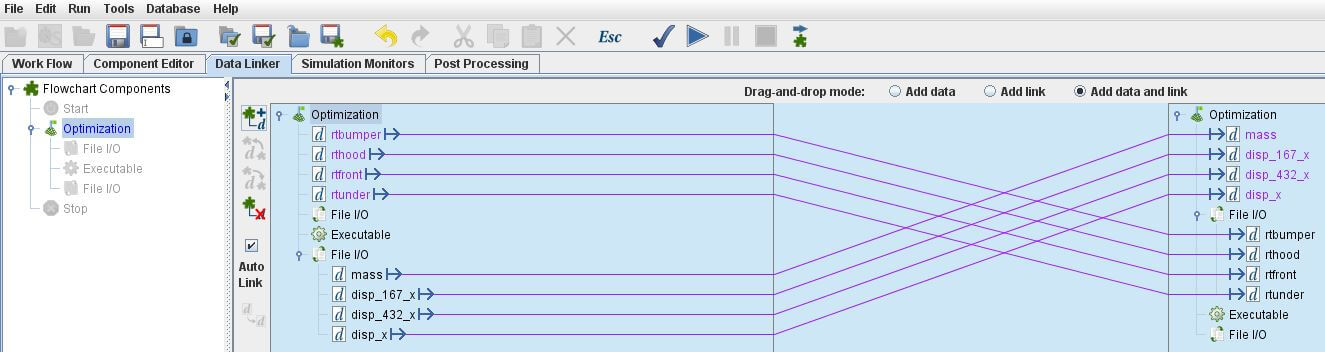
接下來點選C欄中的component editor外層的Optimization component，變數已經新增好了。

5.1.4 Component Editor外層

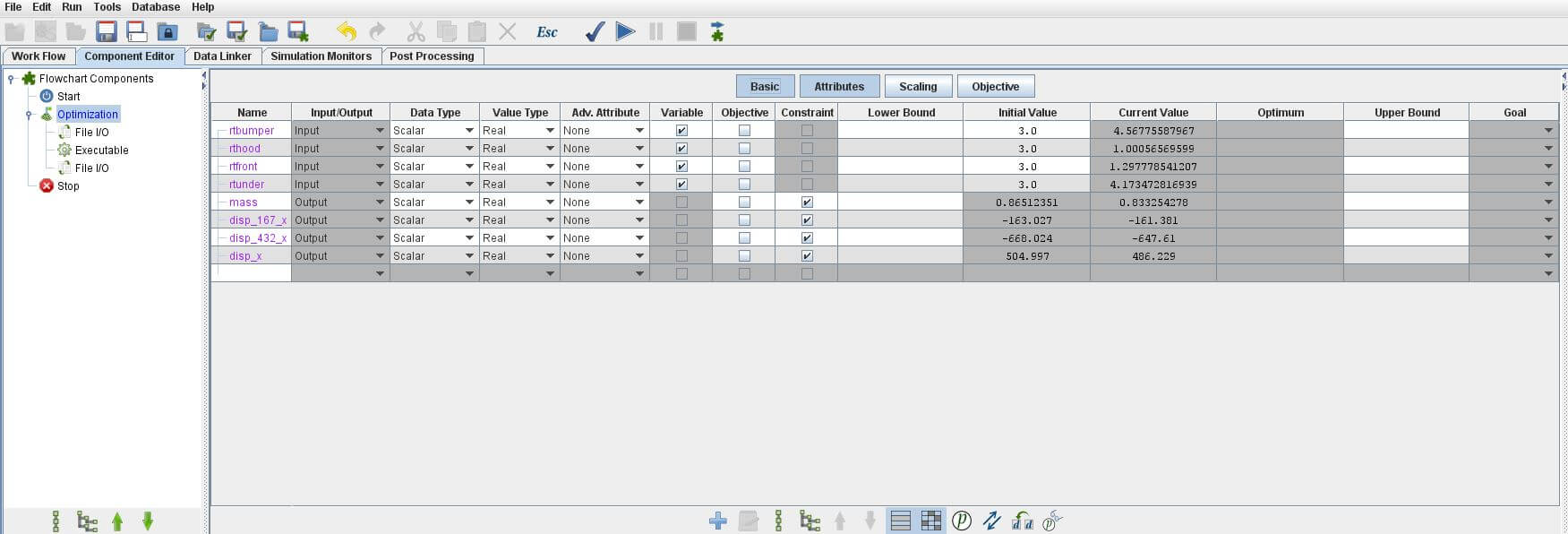
進行下列設定:

• 設定rtbumper、rthood、rtfront及rtunder的Lower Bound為1及Upper Bound為5
• 勾選f為Objective、不勾選其為Constraint，並確定其Goal維持預設的Minimize
• 刪除disp_167_x及disp_432_x
• 勾選disp_x為Constraint，並設定其Upper Bound為485

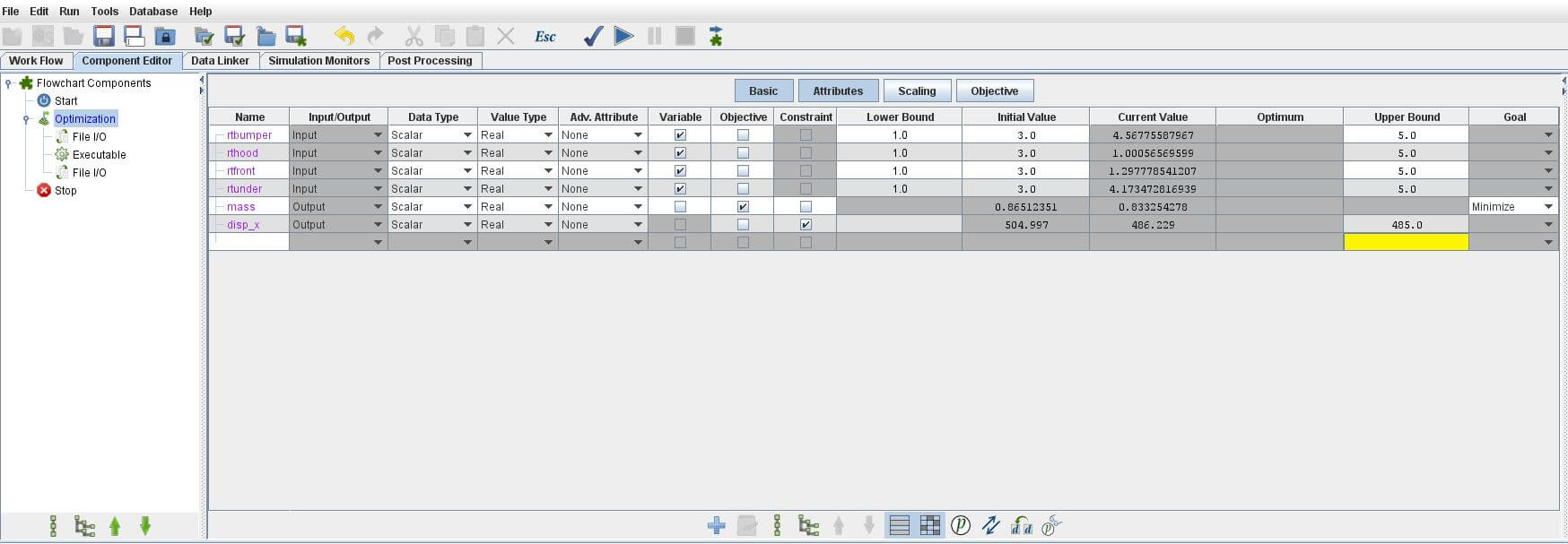
5.1.5 Simulation Monitors

點選C欄 Simulation Monitors，按下右方Add a generic monitor，輸入6，來創造一個觀看6個變數的表格，分別觀察rtbumper、rthood、rtfront、rtunder、mass及disp_x。

接著新增BestObjetive及WrostConstraint這兩個monitor。

手動完成連接後，應該會像:

5.1.6 Post Processing

這是老駱試了幾次之後，比較好的答案，另存一task，命名為Opt good。

這是老駱試了幾次之後，比較差的答案，另存一task，命名為Opt bad。

()內為LS-DYNA運行次數 Unit: ton & mm	tbumper	thood	tfront	tunder	mass	disp
LS-OPT(49)	4.83	1.00	1.00	4.53	0.871	483.216
Baserun(1)	3.00	3.00	3.00	3.00	0.865	504.997
Opt good(207)	4.56	1.00	1.30	4.17	0.833	486.276
Opt bad(93)	4.18	3.27	3.70	4.01	1.091	486.144

LS-DYNA由於考慮其計算效率，所以每次計算的結果，即使是用同一台電腦及同樣的CPU數，跑同樣的問題，也會有微小的差異。在一般的顯性問題中，這樣的誤差是可以接受的。但在跑最佳化問題時，會容易在最佳解附近振盪，花費許多計算資源在等結果收斂，甚至有時候收斂的答案離最佳解還有一段不小的距離。簡單講，直接與LS-DYNA進行Optimization的話，每次跑可能都不同的答案，有時答案很好，有時卻會很差(例如Opt good與Opt bad)。所以老駱一般不建議直接進行Optimization，而是用DOE搭配Optimization或RSA來求解，才是比較實務的作法。

5.2 DOE

開啟Opt good task，另存一task，命名為DOE with responses Composite。將2個File I/O及1個Executable component置入DOE component中，並刪除Optimization component，最後完成work flow連接。步驟與 VDOC_02_DOE 類似。

點選DOE component進行下列設定:

• 設定rtbumper、rthood、rtfront及rtunder的Lower Bound為1及Upper Bound為5，並設定為Variable。
• 勾選mass及disp_x為Response。
• 刪除disp_167_x及disp_432_x。
• DOE Action選擇Create DOE points with responses。
• Designs選擇Composites，共產生25個點位。
• 勾選Reuse approximation from first invocation when run as subflow。

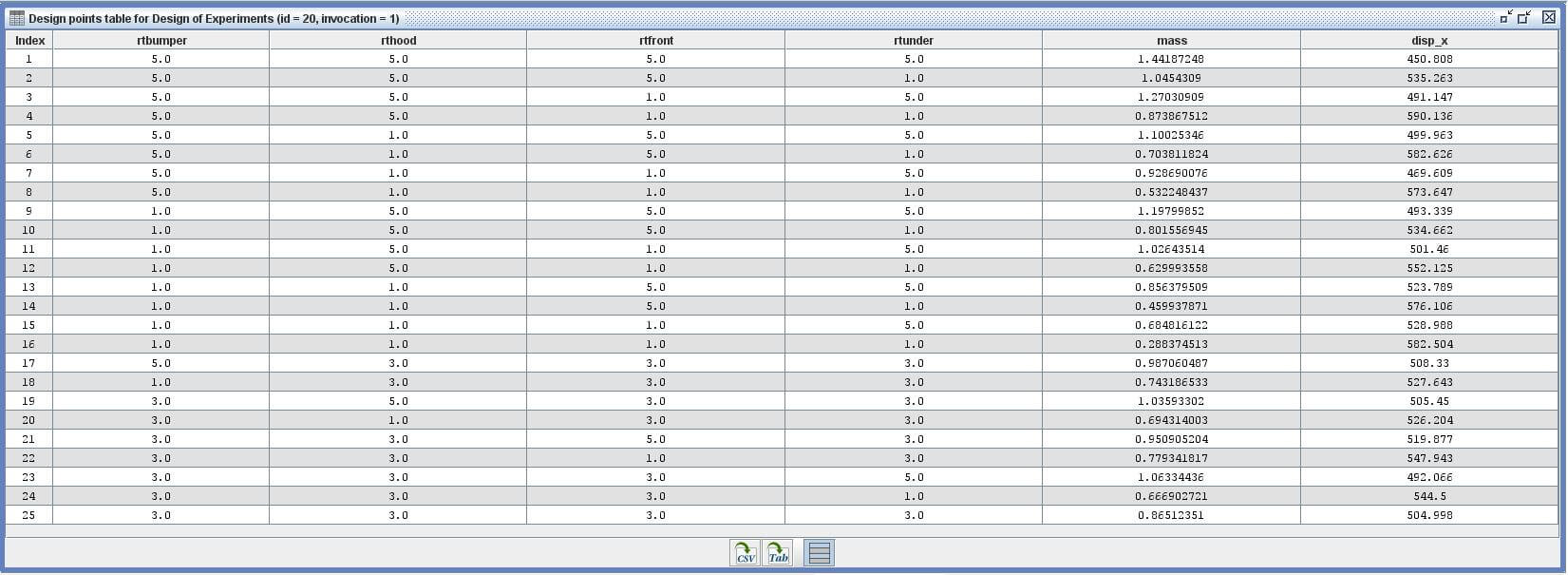
5.3 Optimization Using DOE

開啟DOE with responses Composite task，另存一task，命名為Opt Using DOE。 將DOE component置入Optimization component中並完成work flow連接。

點選DOE component後可以使用User Defined的功能，讀入DOE with responses Composite task產生的25個點位，並將DOE Action改為Create DOE with approximations。

其餘Data Linker、Optimization component 及Simulation Monitors設定與 5.1 Optimization 類似。

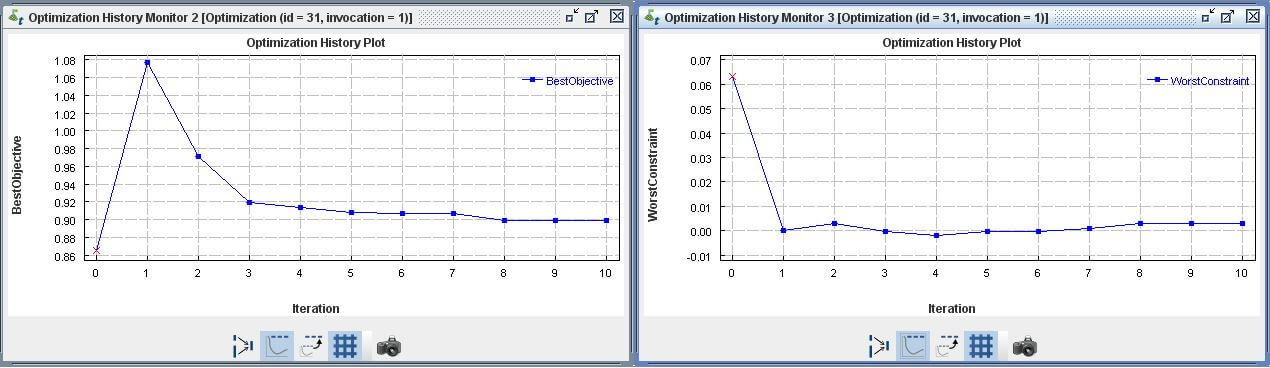
()內為LS-DYNA運行次數 Unit: ton & mm	tbumper	thood	tfront	tunder	mass	disp
LS-OPT(49)	4.83	1.00	1.00	4.53	0.871	483.216
Baserun(1)	3.00	3.00	3.00	3.00	0.865	504.997
Opt good(207)	4.56	1.00	1.30	4.17	0.833	486.276
Opt bad(93)	4.18	3.27	3.70	4.01	1.091	486.144
Opt Using DOE(25)	4.07	1.00	1.64	5.00	0.899	486.404

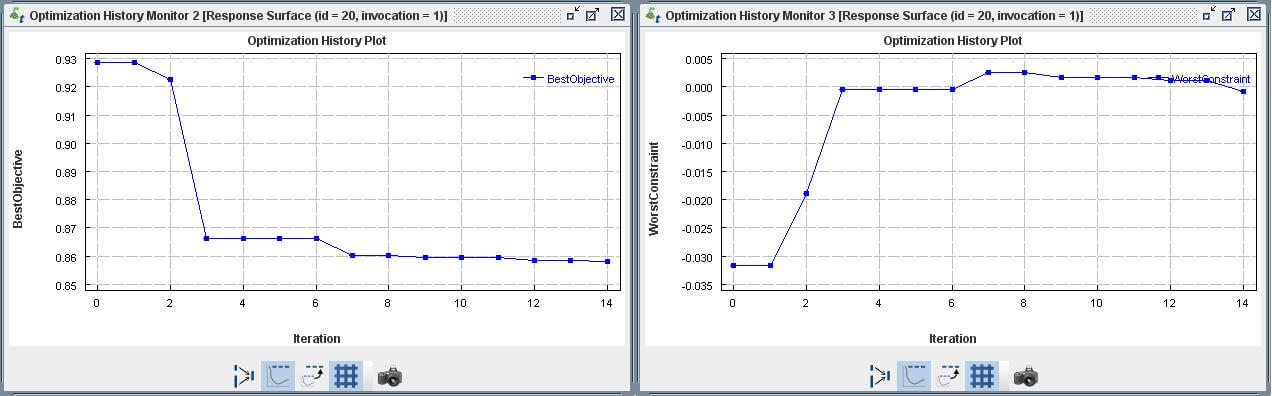
5.4 RSA Using DOE

開啟Opt good task，另存一task，命名為RSA Using DOE。將2個File I/O及1個Executable component置入RSA component中，並刪除Optimization component，最後完成work flow連接。

點選RSA component後可以使用User Defined的功能，讀入DOE with responses Composite task作為Starting Strategy。

其餘Data Linker、RSA component 及Simulation Monitors設定與 5.1 Optimization 類似。

()內為LS-DYNA運行次數 Unit: ton & mm	tbumper	thood	tfront	tunder	mass	disp
LS-OPT(49)	4.83	1.00	1.00	4.53	0.871	483.216
Baserun(1)	3.00	3.00	3.00	3.00	0.865	504.997
Opt good(207)	4.56	1.00	1.30	4.17	0.833	486.276
Opt bad(93)	4.18	3.27	3.70	4.01	1.091	486.144
Opt Using DOE(25)	4.07	1.00	1.64	5.00	0.899	486.404
RSA Using DOE(52)	4.39	1.00	1.30	4.53	0.858	484.591

6. 結語

• 直接使用Optimization來coupleLS-DYNA，須要耗費較多的計算資源，且不保證每次都能得到滿意的答案。
• 使用Optimization+DOE來coupleLS-DYNA，僅須要在DOE時呼叫LS-DYNA。一旦得到了問題的近似函數，後續的Optimization計算速度非常快，且求得的近似解也有一定的品質，是一個經濟實惠的選擇。
• 使用RSA+DOE來coupleLS-DYNA，除了DOE時，做RSA也要呼叫LS-DYNA，但總呼叫次數52次也差不多等於LS-OPT的49次。比較LS-OPT與RSA Using DOE後，可以發現兩者的答案也相去不遠。
• 使用RSA+DOE來coupleLS-DYNA，應該是一可得最佳解的穩定策略。但此策略的後期，因為須確保收斂，可能會多次呼叫LS-DYNA。也就是說，可能會增加很多求解時間，卻無法帶來相對應的最佳解提升。
• 老駱認為，在適當挑選DOE點位的前提下，使用Optimization+DOE來coupleLS-DYNA，應該是一個不錯的策略。如果覺得所求的近似解不是很滿意，可逐步加入DOE點位，來提升準確度。這樣的操作方式應該會比使用RSA+DOE來得更有效益一些。當然如果使用Optimization+DOE來coupleLS-DYNA求解，過程中可能須要反覆調試，略嫌有些麻煩。至於最終採用什麼策略來解題，得取決於問題的難度、求解所需的精度與使用者所擁有的計算資源及時間來綜合考量。

7. 聯絡老駱

如果您或貴單位:

• 有導入VR&D產品的意願，但是有報價、採購及發票等問題。
• 有教育訓練或顧問需求。
• 有些建言指教。
• 想交個朋友。
  歡迎透過 camel@caeml.ai 聯絡老駱。